Dionysia: Accelerating the Simplex Algorithm
Linear programming is an approach used to optimize linear objective functions with linear constraints. While existing software solutions are quite advanced, the use of linear programming in many latency sensitive industries demonstrates the need for research into hardware accelerated solutions. We focus on a specific algorithm for solving linear programs called Simplex, which represents optimization problems as matrices, and searches for solutions with a series of row and column transformations. To translate this algorithm to hardware we designed Dionysia: a parametrizable architecture inspired by the actor concurrency model, which takes advantage of the structure of the Simplex algorithm to solve linear programs with a high degree of parallelism and minimal data movement.
Motivation
LINEAR programming (LP) has applications in a wide range of industries, from archaeological simulations to high voltage electricity transmission. As general purpose hardware has grown faster and memory has grown larger, linear programs have grown to the scale of tens of thousands of variables and tens thousands of constraints (and beyond). While free and open source solutions exist, commercial solvers such as IBM’s CPLEX and Gurobi’s Gurobi Optimizer are required to handle larger LPs efficiently. Unfortunately these command annual license fees from $2000 to $12000, and to truly take advantage of these software packages the user will also need to invest in high-end hardware.
These high costs provided the initial motivation necessary to explore a potential alternative hardware accelerator solution for LP solving. A hardware approach was chosen as there appears to be very little research into hardware acceleration of LP solvers. While most software solutions make use of a variety of optimization algorithms we will focus on the Simplex algorithm, which provides good average runtime and can be largely parallelized. Additionally, we use AWS EC2 F1 platform to build and deploy our compiled Simplex hardware for use on an FPGA.
Proposed Solution
At first glance the requirement that linear programs use both linear constraints and a linear objective function may seem quite restrictive, however, researchers in many fields have found that even within these constraints, a large number of problems can be modeled. As an example, consider the problem of a student who must allocate hours during a semester between two classes to maximize their GPA, while maintaining their marriage (i.e. not spending every single hour working). One of these classes may be difficult (i.e. it will require many hours), and the other easy. This problem can be expressed as a system of equations.
The Simplex algorithm, developed by George Dantzig in the late 1940s, is the first algorithm for solving this type of constrained optimization [@dantzig]. While faster algorithms now exist, Simplex offers an average polynomial runtime along with properties that map well to hardware. Simplex first adds additional variables, called slack variables, to allow the inequality constraints to become equality constraints, and then maps the optimization into a matrix, called the tableau.
After building the tableau, the Simplex algorithm proceeds by carrying out a number of simple row-wise operations until stopping conditions are detected: (1) Searching for a pivot column, (2) Searching for a pivot row, (3) Pivoting along the pivot row, (4) Pivoting the remaining rows. These steps repeat until either a pivot row or a column can not be found. It is sometimes possible for the algorithm to stall and get stuck at a sub-optimal solution. Notably, these operations do not change the shape of the tableau, and the row operations and row data are mostly independent of each other, providing many parallelism opportunities.
Dionysia is our hardware implementation of the Simplex algorithm. It is built with Chisel 3.2, a hardware design language with a focus on parametrizable design and the generation of optimized circuits, and targets the AWS EC2 F1 FPGA platform.
System Design
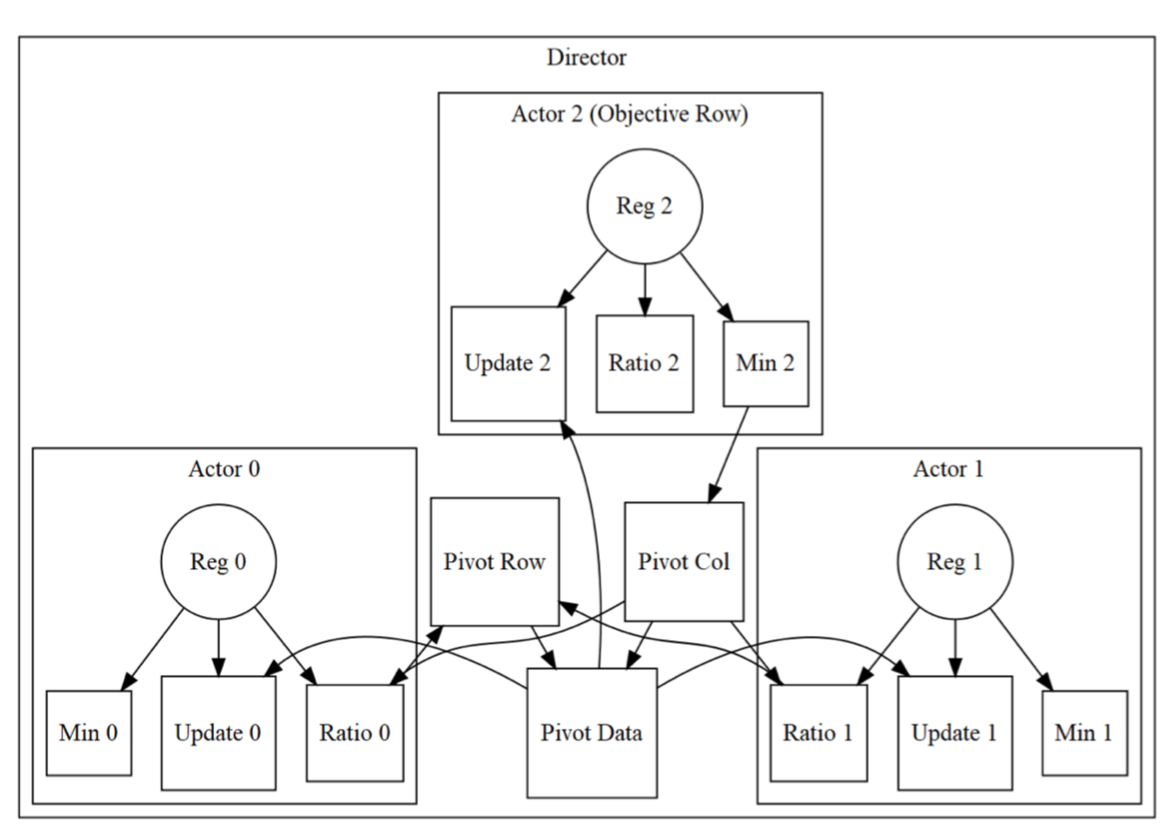
In the context of ancient Greece, Dionysia was a festival largely centered around theater. In this spirit our accelerator, Dionysia, is likewise centered around actors, but in the context of the actor-concurrency model. As such, Dionysia consists of four types of modules: the actor and the director carry out the Simplex algorithm, and the core and subcore manage the FPGAs DRAM and communication with the host. A sketch of the director and actor modules can be seen in the figure above.
The primary control module in Dionysia is the director. This module is responsible for loading data into the actors, issuing instructions to the actors, and monitoring the state of the Simplex algorithm. The director is loosely-coupled with the subcore: it receives data from the subcore and allocates it to each actor, and then waits for a start signal. To carry out the Simplex algorithm the director module uses a nite state machine which cycles through the steps algorithm until a stopping condition is detected. During step (1) the director sets the pivot column to be the index of the minimum positive value for the actor that represents the objective function (the bottom row; Actor 2 in Figure 1). During step (2) the director instructs the actors to compute the ratio between their values at the pivot column index and the constraint value (the last value in the row). The director selects the row with the minimum ratio as the pivot actor. Step (3) updates just the pivot row actor. Step (4) sends the pivot actor’s data to all other actors so that they can update accordingly.
Dionysia instantiates many identical actor modules, each of which is represents a row of the Simplex tableau. Each actor implements a simple finite state machine, where each state represents an independent operation needed to complete the algorithm. These operations include: finding the minimum value, computing the ratio between the constraint value (the final value in the row) and the value in the pivot column, and updating data per the pivot data. The update operation varies per iteration depending on whether or not the actor represents the pivot row. The final actor (in Figure 1 this is Actor 2) represents the objective function; it is the only actor that needs to use the min operation, and does not need the ratio operation. Currently all actors are implemented identically but creating more specialized modules could improve the area-efficiency of Dionysia.
Because this architecture allows actors to operate almost entirely in parallel we achieve strong efficiency: cycle-accurate simulations of Dionysia indicate that each iteration of the Simplex algorithm only requires 25 cycles to complete, regardless of the number of constraints and variables.
Evaluation
We benchmark our accelerator against two popular LP solvers, GLPK and IBM’s CPLEX, as well as a naive implementation of Simplex in R. GLPK is currently the most used open source LP solver. While very versatile, most algorithms supported by GLPK are serial. CPLEX is one of the most popular commercial solvers, unlike GLPK it can take advantage of parallelized optimization methods. CPLEX typically scales well across multicore and distributed systems. The R implementation is completely serial, and mostly used to determine how many iterations of the Simplex algorithm are needed to solve any given problem. The R implementation also serves as a strong argument for not implementing your own LP solver. We allow both GLPK and CPLEX to use any optimization algorithm, not just Simplex. We do this to give a direct comparison between Dionysia and state-of-the-art algorithms with state-of-the-art implementations. All software is run on a shared server with several Xeon E2640 processors (total of 40 cores) and 512Gb of RAM. Our existing benchmarks are based on cycle-accurate simulations shown below.
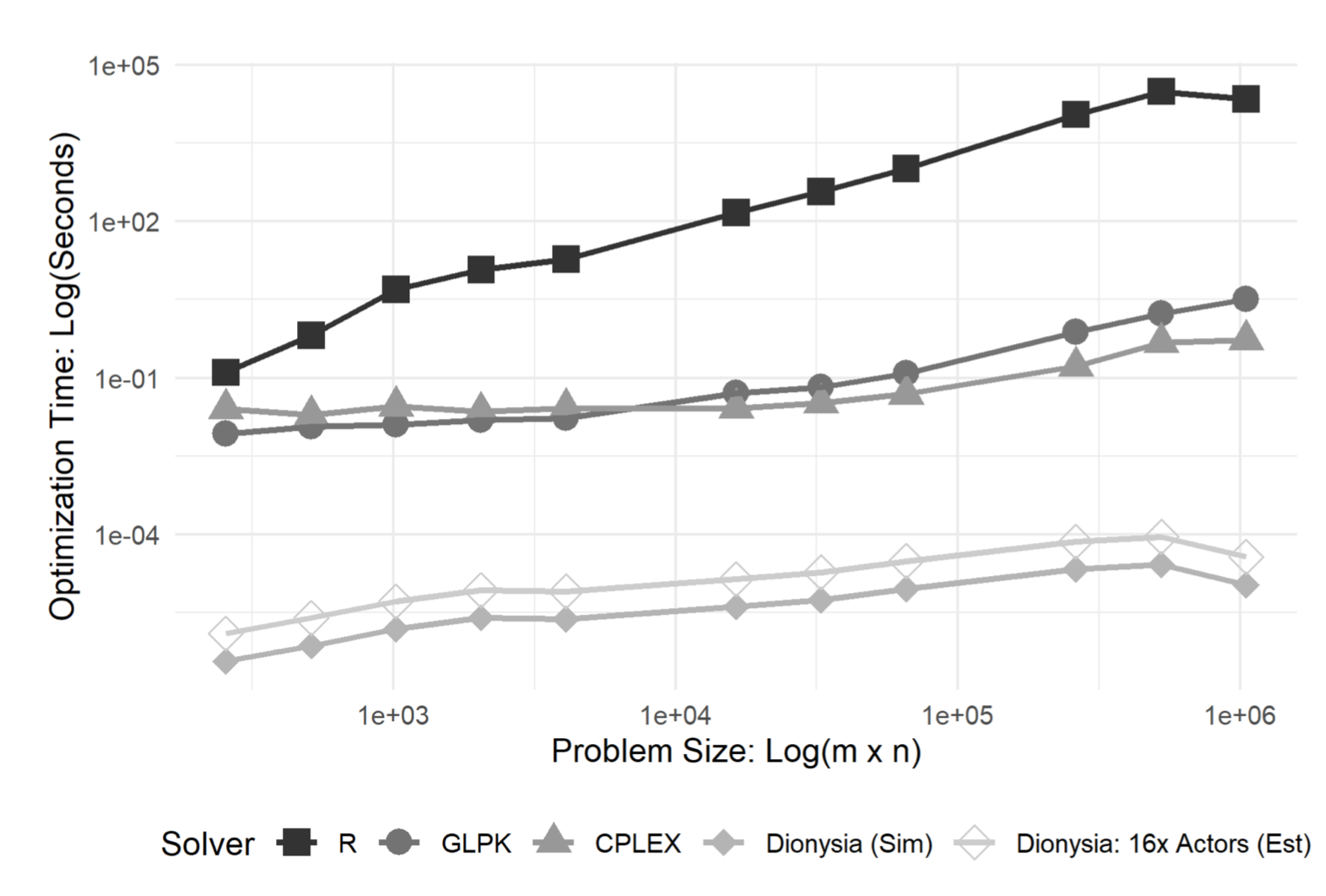
Conclusion
We have provided a simple interface that uses the standard simplex tableau, an accelerator that can be configured to target square (equal number of constraints and variables), tall (more constraints than variables), and wide (more variables than constraints) LP problems. The parallel-memory operations enabled by both designs allows for substantial performance increases compared to state-of-the-art software. While Dionysia has several limiting factors, we believe that the core architecture offers a solid foundation on which to explore further hardware designs.