The Multiple-input multiple-output (MIMO) detector is a critical component that reconstruct the transmitted signals in the modern communication systems. The state-of- the-art Markov Chain Monte Carlo (MCMC) detector shows great potential to achieve optimal performance at low signal- to-noise (SNR), but suffers from degradation at high SNR caused by stalling issues. Hedstrom et al. proposed a novel excited MCMC (X-MCMC) algorithm to solve the high SNR stalling problems. Promising performance of X-MCMC has been corroborated in the software-level simulation, but the hardware implementation has not yet been provided. In this project, we introduce a hardware implementation of X- MCMC detector on an FPGA. We provide a output quality analysis of X-MCMC detector under different floating point precision and the corresponding hardware complexity. Experimental results show that the hardware complexity can be significantly reduced by lowering the floating point decision, which has little impact on the quality of X-MCMC detector.

Motivation

Modern wireless communication protocols, including IEEE 802.11ac (WiFi), 3GPP LTE, 4G LTE, etc., involve multiple-input multiple-output (MIMO) communication systems for the transmission and reception of radio signals. In a typical MIMO system, both the transmitter and receiver have multiple antennas, hence multiple signals in the same channel are transmitted and received simultaneously. This parallel data stream improves the channel capacity, throughput as well as quality, evaluated in terms of bit-error-rate (BER). As a critical component of the receiving terminal, the MIMO detector is utilized to separate and reconstruct the multiplexed signals. The design of a MIMO detector with low SNR and BER is a priority research topic in the construction of a high performance MIMO communication system, especially when the scale of the system is relatively large. The complexity of high performance MIMO detectors tends to increase exponentially with the scale of the system, while less complex detectors usually obtain higher BER in low signal-to-noise ratio (SNR) scenarios. As a consequence, the trade-off between complexity and performance is supposed be addressed in MIMO detector designs. Among state-of-the-art detector designs, the markov chain monte carlo (MCMC) detector outperforms other counterparts owing to its high performance in low SNR scenarios as well as its simplicity for hardware implementations. As a consequence, the MCMC detector has been widely applied in the wireless communication framework, and a series of hardware implementations of the MCMC detector have been proposed based on FPGA, CGRA, and ASIC. The core of the MCMC detector is a Gibbs sampler, which calculates posterior possibility iteratively to estimate the bit sequence of reconstructed signals. However, the performance of MCMC detector in relatively high SNR scenarios degrades due to the fact that the posterior possibility estimation may not converge, which is called high SNR stalling issues. Hedstrom at el. propose an improved version pf MCMC detector named excited MCMC (X-MCMC) detector, which addresses high SNR stalling issues by employing an ”excited Gibbs sampler” to resolve the convergence problems.

X-MCMC outperforms the conventional detector designs and makes X-MCMC a strong candidate for modern MIMO detectors, and since there is no hardware implementation of X-MCMC detector yet, we believe it is worth to implement X-MCMC on hardware to see how X-MCMC actually performs on hardware.

System Design

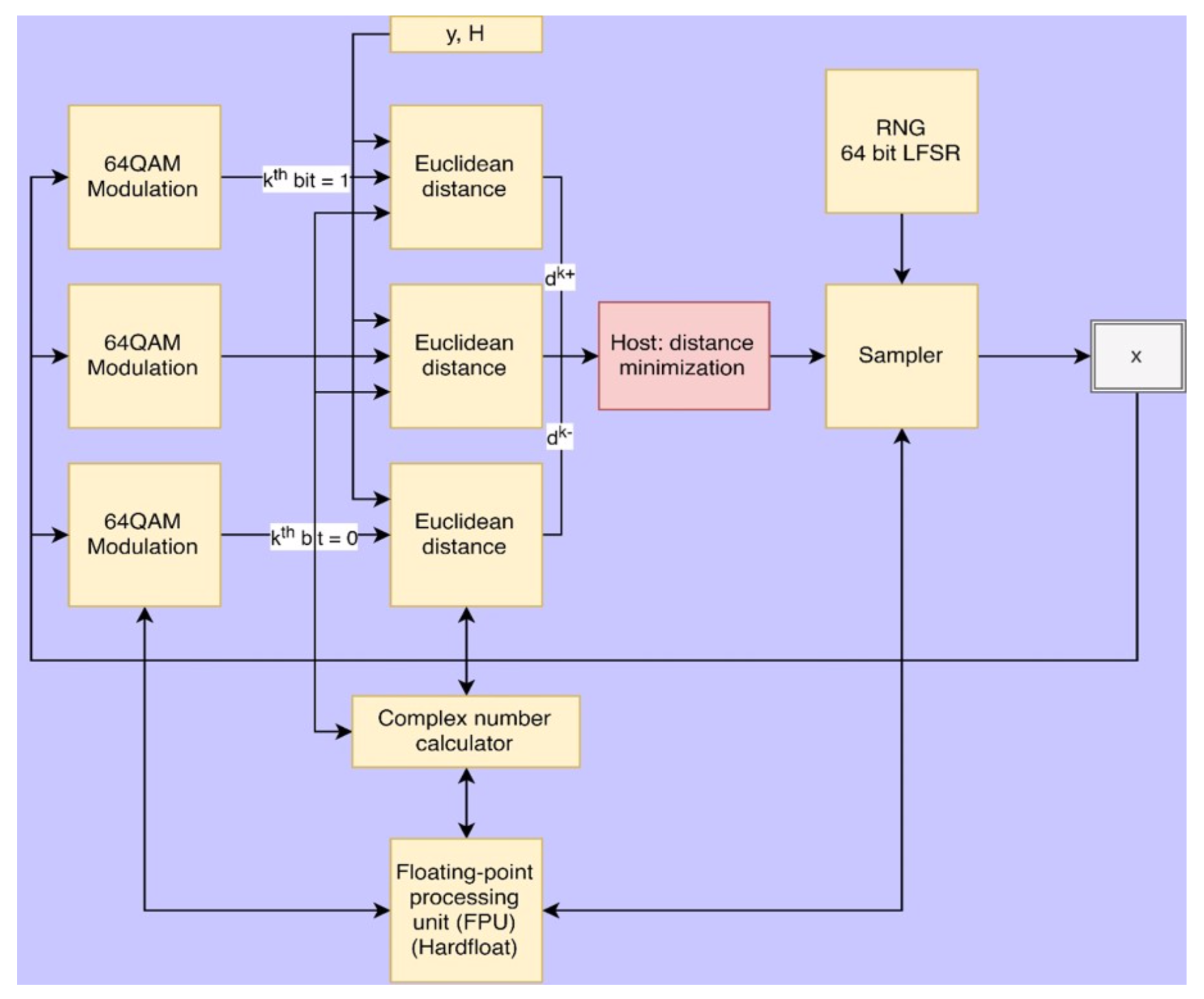
The design block diagram of our X-MCMC implementation is shown in the figure above. The main components include Modulation modules, Euclidean distance modules, a random number generator (RNG) and a Gibbs sampler. Several complex number calculators are instantiated to support the computation executed by Euclidean distance modules, and several floating point processing units (FPUs) are deployed to support the floating point computation in all modules.

The hardware receives input signals vector y and system transition matrix H from the host computer. Modulation modules translate each variation of bit sequence x with the kth bit altered to either a zero or a one to a complex transmission signal vector s, which is Step1 in the X-MCMC algorithm. Euclidean distance modules then calculate the euclidean distances for each Hs to y in complex space (where it uses the Complex Number Calculator module) in Step2. Euclidean distances are then transmitted back to the host for minimization in Step3 ∼ Step5. Given high bandwidth of the PCI-E interface, this process should not be a bottleneck of the performance of this hardware. We have the host computer to compute Step3 ∼ Step5 rather than building dedicated hardware because the computation includes many floating-point divisions, which 1) takes too much engineering effort to build floating-point division unit and debugging, 2) will dramatically increase hardware complexity of the hardware for the complicated floating-point division unit, and 3) takes more than ten cycles of computation thus will add stalls to the data-flow. A comparison of current implementation versus dedicated hardware for Step3 ∼ Step5 remains a future work. The host computer sends the minimized euclidean distance as an input to the Gibbs sampler, and the sampler transforms the euclidean distance to a probability, which is then used to compare with a random number. A inference of kth bit of x will then be generated, correspond- ing to Step6 ∼ Step7. The newly generated x will follow the same process in the next iteration.

Evaluation

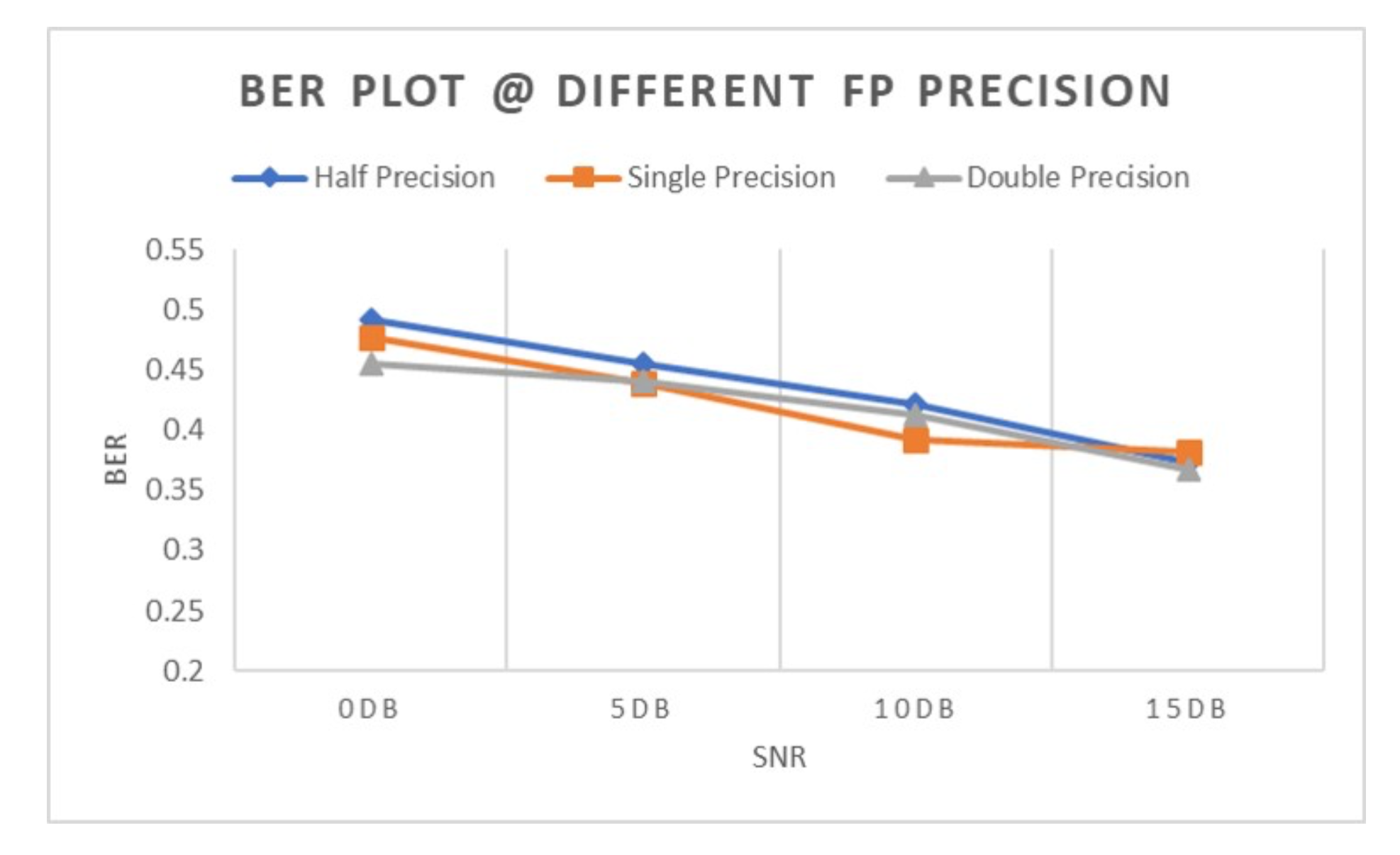
The experiment tests three floating-point precisions: half precision, single precision, and double precision, according to IEEE floating point standards. To generate the data points, we use 3GPP TS 36.211 specifications as a guideline. To obtain test data, we randomly generate bit sequence x and transition matrix H, modulate each x with the mapping included in the specification document to s, then calculate y = Hs + GaussianNoise, where the noise factor varies with SNR. Each design variations are then tested with these data points, generating the inferred x, which is then compared with the original x to obtain BER, which represents the performance on result quality. BERs under different SNRs are then plotted to a BER plot. BER plots are commonly used in MIMO detector studies to characterize the performance of a detector. Three BER curves of the three design variations are plotted together to compare the trend.

Hardware complexity is evaluated by resource utilization of the designs synthesized to the Arria 10 FPGA using Quartus 19.2. Resource utilization includes logic elements used (in ALM) and number of DSP blocks used and results are shown below.

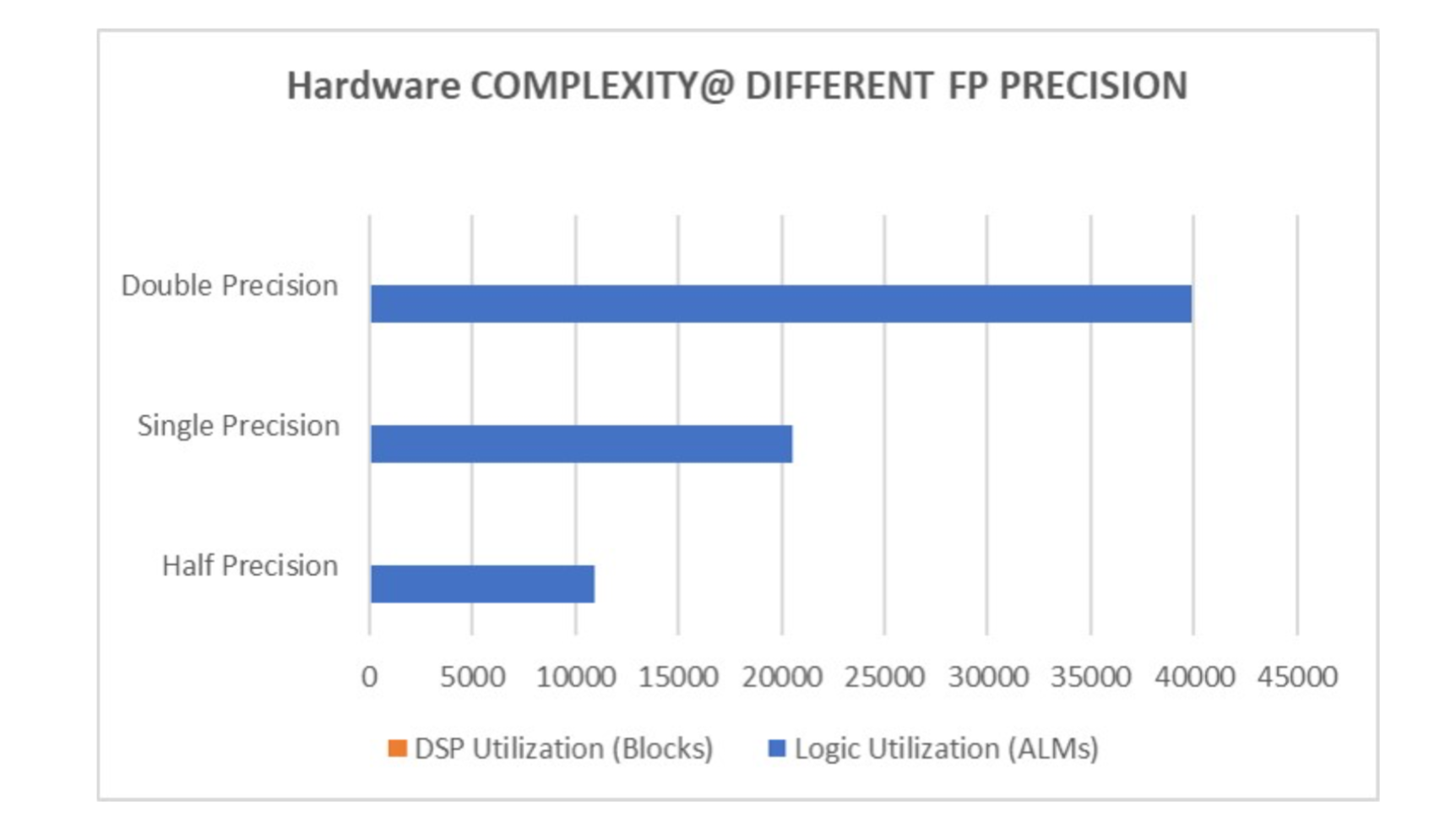
Figure below shows the BER plot of the three design variation based on the preliminary data. As shown in the figure, there are not significant differences between the three curves, leading to the conclusion that floating point precision has little impact on the BER performance of X-MCMC detector.

Conclusion

In this project, we realize the hardware implementation of X-MCMC detector in modern MIMO communication systems on FPGA platform and did preliminary verification. We investigate the BER performance of X-MCMC hardware and discuss the trade-off between hardware complexity and performance. The results clearly show that increasing floating-point precision will significantly increase hardware complexity, while helping very little on BER performance.